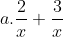AKU SUKA MATEMATIKA: Bentuk Aljabar

Tampilkan postingan dengan label Bentuk Aljabar. Tampilkan semua postingan

Pecahan dalam Bentuk Aljabar

admin ganteng April 04, 2012

admin ganteng

1. Penjumlahan dan Pengurangan Pecahan Bentuk Aljabar
Cara menjumlahkan dan mengurangkan pecahan bentuk aljabar adalah sama dengan menjumlahkan dan mengurangkan pada pecahan biasa, yaitu dengan menyamakan penyebutnya terlebih dahulu.

Contoh 1:
Sederhanakan bentuk penjumlahan berikut:
$a. \frac{2}{x}+\frac{3}{x}$
$b. \frac{4}{3x}+\frac{3}{y}$
$c. \frac{x-1}{x}+\frac{3}{x+1}$

Penyelesaian:

$a. \frac{2}{x}+\frac{3}{x}$	=	$\frac{2+3}{x}=\frac{5}{x}$
$b. \frac{4}{3x}+\frac{3}{y}$	=	$\frac{4.y}{3x.y}+\frac{3.3x}{y.3x}$
	=	$\frac{4y}{3xy}+\frac{9x}{3xy}$
	=	$\frac{4y+9x}{3xy}$
$c. \frac{x-1}{x}+\frac{3}{x+1}$	=	$\frac{(x-1)(x+1)}{x(x+1)}+\frac{3.x}{x(x+1)}$
	=	$\frac{x^2-1}{x(x+1)}+\frac{3x}{x(x+1)}$
	=	$\frac{x^2+3x-1}{x(x+1)}$

2. Perkalian dan Pembagian Pecahan Bentuk Aljabar
Cara menyelesaikan perkalian dan pembagian pecahan bentuk aljabar sama dengan menyelesaikan perkalian dan pembagian pecahan biasa, yaitu

dan

Contoh 2:
Sederhanakan bentuk aljabar berikut:
$a. \frac{24}{xy}:\frac{3}{xy}$
$b. \frac{4x}{x+1}\times \frac{3x-2}{y}$
$c. \frac{x-5}{12}:\frac{x}{4}$

Penyelesaian:

$a. \frac{24}{xy}:\frac{3}{xy}$	=	$\frac{24}{xy}\times\frac{xy}{3}$
	=	$\frac{24xy}{3xy}=8$
$b. \frac{4x}{x+1}\times \frac{3x-2}{y}$	=	$\frac{4x(3x-2)}{y(x+1)}$
	=	$\frac{12x^2-8x}{xy+y}$
$c. \frac{x-5}{12}:\frac{x}{4}$	=	$\frac{x-5}{12}\times\frac{4}{x}$
	=	$\frac{4(x-5)}{12x}$
	=	$\frac{x-5}{3x}$

Pemfaktoran Bentuk Aljabar

admin ganteng Maret 30, 2012

admin ganteng

Bentuk Aljabar Matematika SMP

Pemfaktoran dengan Sifat Distributif
Pada dasarnya, memfaktorkan suatu bilangan berarti menyatakan suatu bilangan dalam bentuk perkalian faktor-faktornya. Pada bagian ini, akan dipelajari cara-cara memfaktorkan suatu bentuk aljabar dengan menggunakan sifat distributif. Dengan sifat ini, bentuk aljabar ax + ay dapat difaktorkan menjadi a(x + y), di mana a adalah faktor persekutuan dari ax dan ay. Untuk lebih jelasnya, pelajarilah Contoh Soal berikut.

Contoh 1:
Faktorkan bentuk-bentuk aljabar berikut.
a. 3pq + 6p
b. 8x – 2x²y
c. –5a²b² + 10ab
d. ¹/₂ x³y² + ¹/₄ x²y³

Penyelesaian:
a. 3pq + 6p
Untuk memfaktorkan 3pq + 6p, tentukan faktor persekutuan dari 3 dan
6, kemudian dari pq dan p. Faktor persekutuan dari 3 dan 6 adalah 3.
Faktor persekutuan dari pq dan p adalah p.
Jadi, 3pq + 6p difaktorkan menjadi 3p(q + 2).
Dengan kata lain 3pq + 6p = 3p(q + 2)

b. 8x – 2x²y
Faktor persekutuan dari 2 dan –8 adalah 2. Faktor persekutuan dari x dan x2y adalah x.
Jadi,8x – 2x²y = 2x(4 – xy).

c. –5a²b² + 10ab
Faktor persekutuan dari –5 dan 10 adalah 5. Faktor persekutuan dari a²b²dan ab adalah ab.
Jadi, –5a²b² + 10ab = 5ab (–ab + 2).

d. ¹/₂ x³y² + ¹/₄ x²y³
Faktor persekutuan dari ¹/₂ dan ¹/₄ adalah ¹/₄.
Faktor persekutuan dari x³y² adalah x²y³ adalah x²y².
Jadi, ¹/₂ x³y² + ¹/₄ x²y³ = ¹/₄ x²y² (2x +y)

Selisih Dua Kuadrat (a²- b²)
Perhatikan bentuk perkalian berikut:

(a + b)(a – b)	=	a(a – b) + b(a – b)
	=	a² - ab + ab - b²
	=	a²- b²

Jadi, bentuk a²- b² dapat dinyatakan dalam bentuk:

Contoh 2 :
Faktorkan bentuk-bentuk berikut.
a. y² – 9
b. 16x² – 4y²
c. 25 p² – 9q²
d. 20x² – 5y²
Penyelesaian:

a.	y² – 9	= y² – 3²
		= (y + 3)(y - 3)
b.	16x² – 4y²	= 4²x² - 2²y²
		= (4x + 2y)(4x - 2y)
c.	25 p² – 9q²	= 5²x² - 3²y²
		= (4x + 2y)(4x - 2y)
d.	20x² – 5y²	= 5(4x² – y²)
		= 5(2²x² - y²)
		= 5(2x + y)(2x - y)

Pemfaktoran Bentuk Kuadrat
a. Dengan a = 1
Masih ingat dengan bentuk perkalian aljabar berikut??

(x + p)(x + q)	=	x(x + q) + p(x + q)
	=	x² + qx + px + pq
	=	x² + (q + p)x + pq

Nah, jika kita perhatikan bentuk diatas, tenyata bentuk x² + (q + p)x + pq dapat kita faktorkan menjadi (x + p)(x + q).
Misalkan x² + (q + p)x + pq = ax² + bx + c, dengan a=1, b = p+q dan c = p.q
dari permisalan diatas, dapat dilihat bahwa p dan q merupakan faktor dari c. Jika p dan q dijumlahkan, hasilnya adalah b. Dengan demikian untuk memfaktorkan bentuk ax2 + bx + c dengan a = 1, tentukan dua bilangan yang merupakan faktor dari c dan apabila kedua bilangan tersebut dijumlahkan, hasilnya sama dengan b.
Perhatikan contoh soal berikut.

Contoh 3:
Faktorkanlah bentuk-bentuk berikut.
a. x² + 5x + 6
b. x² – 3x + 2
c. x² + 2x – 8

Penyelesaian:
a. x² + 5x + 6

Langkah pertama untuk memfaktorkan persamaan di atas, adalah dengan menententukan dua bilangan yang merupakan faktor dari 6, yang apabila kedua bilangan tersebut dijumlahkan, hasilnya sama dengan 5.
Faktor dari 6 adalah ±6 dan ±1 atau ±2 dan ±3, yang memenuhi syarat adalah 2 dan 3
Jadi, x² + 5x + 6 = x² + (2+3)x + 2.3 = (x + 2)(x + 3)

b. x² + 3x + 2

tentukan dua bilangan yang merupakan faktor dari 2, yang apabila kedua bilangan tersebut dijumlahkan, hasilnya sama dengan 3.
Faktor dari 2 adalah ±2 dan ±1
Jadi, x² – 3x + 2 = x² – (2 +1)x + 2.1 = (x – 2)(x – 1)

c. x² + 2x – 8
tentukan dua bilangan yang merupakan faktor dari 8, yang apabila kedua bilangan tersebut dijumlahkan, hasilnya sama dengan 2.
Faktor dari 8 adalah ±1, ±2, ±4, dan ±8.
Jadi, x² + 2x - 8 = x² + (4+(-2))x + 4.(-2) = (x + 4)(x - 2)

Dari contoh diatas (contoh 3a.) dapat kita simpulkan bahwa faktor dari x² + 5x + 6, dapat ditentukan dari dua bilangan yang jika dijumlahkan menghasilkan 5 (koefisien dari x), dan jika dikalikan menghasilkan 6, dua bilangan tersebut adalah 2 dan 3.
Dengan demikian x² + 5x + 6 = (x + 2)(x + 3)
Begitu pula untuk contoh 3b dan 3c.

b. Dengan a ≠ 1
Untuk menyelesaikan bentuk pemfaktoran dari ax² + bx + c, terlebih dahulu kalikan nilai a (koefisien dari x²) dengan c. Kemudian tentukan dua bilangan yang apabila dikalikan menghasilkan ac dan apabila dijumlahkan menghasilkan b.

Contoh 4:
Faktorkanlah bentuk dari 2x² + 5x + 2
Penyelesaian:

Koefisien dari x² adalah 2, dan konstanta pada persamaan diatas adalah 2, jika kedua bilangan ini dikalikan hasilnya 4. Tentukan dua bilangan yang jika dikalikan hasilnya 4, sedangkan jika dua bilangan itu dijumlahkan hasilnya 5 (koefisien dari x). Kedua bilangan itu adalah 1 dan 4. sehingga:

2x² + 5x + 2	=	2x² + (1 + 4)x + 2
	=	2x² + 1x + 4x + 2
	=	x(2x + 1) + 2(2x + 1)
	=	(x + 2)(2x + 1)

Contoh 5:
Faktorkanlah bentuk dari 3x² - x - 10
Penyelesaian:

Koefisien dari x² adalah 3, dan konstanta pada persamaan diatas adalah (-10), jika kedua bilangan ini dikalikan hasilnya (-30). Tentukan dua bilangan yang jika dikalikan hasilnya (-30), sedangkan jika dua bilangan itu dijumlahkan hasilnya -1 (koefisien dari x). Kedua bilangan itu adalah 5 dan (-6). sehingga:

3x² - x - 10	=	3x² + (-6 + 5)x - 10
	=	3x² - 6x + 5x + - 10
	=	3x(x - 2) + 5(x - 2)
	=	(3x + 5)(x - 2)

Bentuk Aljabar (bagian 2)

admin ganteng Maret 29, 2012

admin ganteng

Pada postingan sebelumnya, kita telah mempelajari definisi bilangan berpangkat. Pada kesempatan kali ini materi tersebut akan dikembangkan, yaitu memangkatkan bentuk aljabar.

Perpangkatan bentuk aljabar
Seperti yang telah kita ketahui, bilangan berpangkat didefinisikan sebagai berikut.

aⁿ= a x a x a x ... x a (sebanyak n kali)

Untuk a bilangan riil dan n bilangan asli.
Definisi bilangan berpangkat berlaku juga pada bentuk aljabar. Untuk lebih jelasnya, pelajari contoh berikut.

Contoh:
a³ = a x a x a
4² = 4 x 4
2⁴ = 2 x 2 x 2 x 2
(2a)³ = 2a × 2a × 2a = (2 × 2 × 2) × (a × a × a) = 8a³
(–3p)⁴ = (–3p)×(–3p)×(–3p)×(–3p)= 81p⁴

Lalu, bagaimana dengan bentuk (a + b)²?
Bentuk (a + b)² merupakan bentuk lain dari (a + b) (a + b). Jadi, dengan menggunakan sifat distributif, bentuk (a + b)² dapat ditulis:

(a + b)²	=	(a + b) x (a + b)
	=	a(a + b) + b(a + b)
	=	a² + ab + ab + b²
	=	a² + 2ab + b²

Dengan cara yang sama, bentuk (a - b)² juga dapat ditulis:

(a - b)²	=	(a - b) x (a - b)
	=	a(a - b) - b(a - b)
	=	a² - ab - ab + b²
	=	a² - 2ab + b²

Dari uraian diatas maka didapatkan bentuk:

(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²

Contoh 1:
Tentukan hasil kuadrat dari bentuk aljabar berikut:
(3x + 5)²
Penyelesaian:

(3x + 5)²	=	(3x)² + 2(3x)(5) + (5)²
	=	9x² + 30x + 25

Contoh 2:
Tentukan hasil kuadrat dari bentuk aljabar berikut:
(2x - 3)²
Penyelesaian:

(2x - 3)²	=	(2x)² - 2(2x)(3) + (3)²
	=	4x² - 12x + 9

Bentuk Aljabar (bagian I)

admin ganteng Maret 27, 2012

admin ganteng

Bentuk 3a, p³, 4x² adalah salah satu contoh bentuk aljabar. Pada bentuk aljabar 3a, 3 disebut koefisien dan a disebut varibel. Untuk bentuk aljabar yang koefisiennya satu, biasanya tidak ditulis. Misalnya 1a = a
4a = 4 x a = a + a + a + a
3b = 3 x b = b + b + b
a²= a x a

Penjumlahan dan pengurangan bentuk aljabar
Untuk menyelesaikan bentuk aljabar yang mempunyai beberapa suku sejenis, maka suku suku yang sejenis dikelompokkan menjadi satu.
Pada dasarnya, sifat-sifat penjumlahan dan pengurangan yang berlaku pada bilangan riil, berlaku juga untuk penjumlahan dan pengurangan pada bentuk-bentuk aljabar, sebagai berikut.
a. Sifat Komutatif
a + b = b + a, dengan a dan b bilangan riil
b. Sifat Asosiatif
(a + b) + c = a + (b +c), dengan a, b, dan c bilangan riil
c. Sifat Distributif
a (b + c) = ab + ac, dengan a, b, dan c bilangan riil

Contoh 1;
Sederhanakan bentuk-bentuk aljabar berikut.
a. 2a + 3a
b. 11x + 2 + 3x + 4
c. –2x – 3y + 5x – 1
d. 3p – 2p² + 4q – 3q² + p
e. 2m + 3(m² – n²) – m² + 3n²
f. 5mn + 3mn
g. 2x + 3y + 5x – y

Jawab

a.	2a + 3a	= (2+3)a = 5a
b.	11x + 2 + 3x + 4	= 11x + 3x + 2 + 4 = 14x + 6
c.	–2x – 3y + 5x – 1	= –2x + 5x – 3y – 1 = 3x –3y – 1
d.	3p – 2p²+ 4q – 3q² + p	= 3p + p – 2p² + 4q – 3q²
		= 4p – 2p² + 4q – 3q² = –2p² + 4p – 3q² + 4q
e.	2m + 3(m² – n²) – m² + 3n²	= 2m + 3m² – 3n² – m² + 3n²
		= 2m + 3m² – m² – 3n² + 3n²
		= 2m²+ 2m
f.	5mn + 3mn	= 8mn
g.	2x + 3y + 5x – y	= 2x + 5x + 3y - y = 7x + 2y

Perkalian suku-suku aljabar
3 x a = 3a
a x b = ab
axa=a²

Operasi perkalian pada aljabar bisa mengunakan sifat distributif. Sifat distributif merupakan konsep dasar perkalian pada bentuk aljabar. Untuk lebih jelasnya, pelajari contoh berikut.

Contoh 2:
Selesaikan perkalian berikut.
a. 2(x + 3)
b. –5(9 – y)
c. 3x(y + 5)
d. –9p(5p – 2q)

Jawab:
a. 2(x + 3) = 2x + 2(3) = 2x + 6
b. –5(9 – y) = -5(9) -5(-y) = –45 + 5y
c. 3x(y + 5) = 3x(y) + 3x(5) = 3xy + 15x
d. –9p(5p – 2q) = -9p(5p) -9p(-2q) = –45p2 + 18pq

Contoh 3:
Tentukan hasil perkalian suku dua berikut, kemudian sederhanakan.
a. (x + 3)(x + 2)
b. (x – 6)(x + 1)
c. (2x + 3)(4x + 1)

Jawab:

a.	(x + 3)(x + 2)	= (x + 3)x + (x + 3)2
		= x² + 3x + 2x + 6
		= x² + 5x + 6
b.	(x – 6)(x + 1)	= (x – 6)x + (x – 6)1
		= x² – 6x + x – 6
		= x² – 5x – 6
c.	(2x + 3)(4x + 1)	= (2x + 3)4x + (2x + 3)1
		= 8x² + 12x + 2x + 3
		= 8x² + 14x + 3