Tampilkan postingan dengan label Problem set. Tampilkan semua postingan
Tampilkan postingan dengan label Problem set. Tampilkan semua postingan
Pembahasan Problem Set 3 - Dasar (no.11-15)
admin ganteng
Pembahasan Problem Set 3 - Dasar (no.6-10)
admin ganteng
Pembahasan Problem Set 3 - Dasar (no1-5)
admin ganteng
Pembahasan Problem Set 1 - Dasar (no.21-25)
admin ganteng
no.21
x2 – 9x+k = 0 , dengan akar-akar p dan q
p+q = 9 → p = 9 – q
p, q, (p+q+3) Membentuk barisan Geometri
q2=p.12
q2=(9–q).12
q2+12q–12.9=0
(q+18)(q–6)=0
q=–18 atau q=6
no.22
1/2 log(2x-1)≥ 1/4 log x
2-1 log(2x-1)≥ 2-2 log x
- 2log(2x-1)≥(-1/2)2log x
2 2log(2x-1)≤ 2log x
(2x-1)2 ≤ x
4x2 - 5x + 1 ≤ 0
(x-1)(4x-1) ≤0



no.23
a=3, r=2, dan S(n+2) = 381
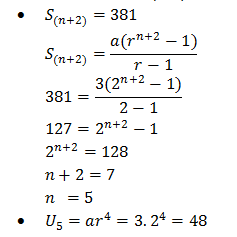
no.24

Sehingga:

no.25
f(x)=2x
Sehingga:
x2 – 9x+k = 0 , dengan akar-akar p dan q
p+q = 9 → p = 9 – q
p, q, (p+q+3) Membentuk barisan Geometri
q2=p.12
q2=(9–q).12
q2+12q–12.9=0
(q+18)(q–6)=0
q=–18 atau q=6
| * | Untuk q = –18 → p = 27 | |
| |p–q|=|27-(-18)|=45 | ||
| * | Untuk q = –18 → p = 27 | |
| |p-q|=|3-(6)|=3 |
no.22
1/2 log(2x-1)≥ 1/4 log x
2-1 log(2x-1)≥ 2-2 log x
- 2log(2x-1)≥(-1/2)2log x
2 2log(2x-1)≤ 2log x
(2x-1)2 ≤ x
4x2 - 5x + 1 ≤ 0
(x-1)(4x-1) ≤0



no.23
a=3, r=2, dan S(n+2) = 381
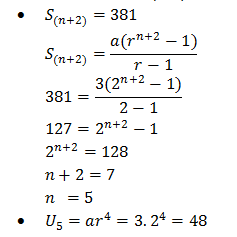
no.24

Sehingga:

no.25
f(x)=2x
Sehingga:
| f(x)+f(x+1)+f(x+2)+f(x+3) | = | 2x + 2x+1+ 2x+2+ 2x+3 |
| = | 2x+ 2.2x+ 4.2x+ 8.2x | |
| = | (1+2+4+8)2x | |
| = | 15.2x | |
| = | 15.f(x) |
Pembahasan Problem Set 1 - Dasar (no.16-20)
admin ganteng
Pembahasan Problem Set 1 - Dasar (no.11-15)
admin ganteng
Pembahasan Problem Set 1 - Dasar (no.6-10)
admin ganteng
no. 6

no. 7
x2 – x + 2 = 0
p+q = 1 dan p.q = 2
Persamaan kuadrat baru dengan akar-akar: (2p – 3) dan (2q – 3)
Persamaan kuadrat baru tersebut adalah:
x2 + 4x + 11 = 0
no. 8
y = ax2 + 2x + a2 + 2a
no. 9

sehingga

no. 10
Banyak kemungkinan = 3.3!=3.3.2.1=18

no. 7
x2 – x + 2 = 0
p+q = 1 dan p.q = 2
Persamaan kuadrat baru dengan akar-akar: (2p – 3) dan (2q – 3)
| (2p-3) + (2q-3) | = | 2(p+q)-6 |
| = | 2 – 6 = – 4 | |
| (2p – 3)(2q – 3) | = | 4pq – 6(p+q) +9 |
| = | 4(2) – 6(1) + 9 = 11 |
x2 + 4x + 11 = 0
no. 8
y = ax2 + 2x + a2 + 2a
| * | Memotong di (0,3) | |
| 3 = a2 + 2a | ||
| a2 + 2a – 3 = 0 | ||
| (a – 1)(a+3)=0 | ||
| a = 1 atau a = – 3 | ||
| * | Untuk a = 1 | |
| y = x2 + 2x + 3 | ||
| | ||
| | ||
| Minimum (-1,2) |
no. 9

sehingga

no. 10
Banyak kemungkinan = 3.3!=3.3.2.1=18
Pembahasan Problem Set 1 - Dasar (no1-5)
admin ganteng
no. 1

no. 2
Ralat Soal
no. 3
no. 4
Karena garis g dan h saling tegak lurus, maka mg. mh= – 1
no. 5



no. 2
Ralat Soal
no. 3
| cos2 (30◦) + cos2 (40◦) + cos2 (50◦) + cos2 (60◦) | ||
| = cos2 (30◦) + cos2 (40◦) + sin2 (40◦) + sin2 (30◦) | ||
| = 1 + 1 = 2 |
no. 4
| g: (a + 2) + y(a – 2 )=0 | → | |
| h: x(-1-3a)+y(5+3a)=5 | → | |
Karena garis g dan h saling tegak lurus, maka mg. mh= – 1
| | = | – 1 |
| – (a+2)(1+3a) | = | –( a–2)(3a+5) |
| 3a2 + 7a + 2 | = | 3a2 – a – 10 |
| 8a | = | – 12 |
| a | = | – 1,5 |
no. 5


Langganan:
Postingan (Atom)

































