Syarat Segitiga-Segitiga Sebangun

Pada Gambar di bawah tampak dua segitiga, yaitu ∆ ABC dan ∆ KLM.


Perbandingan panjang sisi-sisi yang bersesuaian pada kedua segitiga tersebut adalah sebagai berikut:



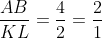
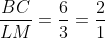
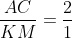
Dengan demikian, diperoleh :



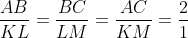
Jika sudut-sudut dari kedua segitiga itu kita ukur, maka sudut-sudut yang bersesuaian akan sama besar yaitu ﮮ A dengan ﮮ K. ﮮ B dengan ﮮ L, dan ﮮ C dengan ﮮM dengan kata lain ﮮ A = ﮮ K, ﮮ B = ﮮ L dan ﮮ C = ﮮ M
Karena sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai dan sudut yang bersesuaian sama besar maka ∆ ABC dan ∆ KLM sebangun.

Konsep kesebangunan dua segitiga dapat digunakan untuk menghitung panjang salah satu sisi segitiga sebangun yang belum diketahui. Untuk lebih jelas, Coba perhatikan contoh berikut!

Contoh 1:


JIka ∆ABC sebangun dengan ∆KLM. Tentukan panjang AB ?
Penyelesaian:




Contoh 2:

JIka ∆ABC sebangun dengan ∆PQR. Tentukan nilai a dan b ?

Penyelesaian:
Perbandingan sisi-sisi kedua segitiga tersebut adalah

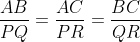
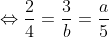
sehingga:

Garis-Garis Sejajar pada Sisi Segitiga

Pada Gambar Di atas, ∆ PQR dan ∆ STR sebangun.
Dari gambar tersebut terlihat bahwa garis DE // AB sehingga diperoleh
ﮮ PRQ = ﮮ SRT (berimpit)
ﮮ RPQ = ﮮ RST (sehadap)
Karena dua sudut yang bersesuaian dari ∆ PQR dan ∆ STR sama besar maka kedua segitiga itu sebangun. Karena sebangun maka berlaku


Dari perbandingan sisi-sisi segitiga di atas, diperoleh

	=
	=
bc + bd	=	ad + bd
bc	=	ad
	=

Contoh:

Jika garis PT//QS, tentukanlah panjang PS.

Penyelesaian:

	=
	=
PS	=	3 x 3 = 9

Dua Bangun Datar yang Sebangun

Dua bangun datar dikatakan sebangun jika memenuhi dua syarat berikut.
1. Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai.
2. Sudut-sudut yang bersesuaian sama besar.



Perhatikan Gambar di atas. Trapesium ABCD dan PQRS mempunyai sisi-sisi yang bersesuaian, yaitu:
AB dengan PQ
BC dengan QR
CD dengan RS
AD dengan PS

Panjang sisi kedua trapesium tersebut mempunyai perbandingan yang senilai. yaitu:





Dengan demikian, sisi-sisi yang bersesuaian dari kedua persegi panjang mempunyai perbandingan yang sama, yaitu


kedua trapesium tersebut mempunyai sudut-sudut yang bersesuaian sama besar, yaitu
ﮮ A = ﮮP, ﮮ B = ﮮQ, ﮮC = ﮮ R. dan ﮮ D = ﮮ S
Dapat dikatakan bahwa trapesium ABCD sebangun dengan trapesium PQRS dan ditulis ABCD ~ PQRS.

Kongruen

Dua Bangun yang Kongruen.
Bangun-bangun geometri dikatakan kongruen (sama sebangun) jika dan hanya jika bangun-bangun itu mempunyai sisi-sisi bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar. Dengan kata lain bangun geometri dikatakan kongruen juka ukuran dan bentuknya yang sama. Jika tidak memenuhi salah satu saja, maka bangun tersebut tidak kongruen.
Perhatikan contoh dua bangun di bawah ini


Dua Segitiga yang Kongruen.
Segitiga yang kongruen adalah segitiga yang bentuknya sama dan ukurannya sama. Tetapi karena segitiga merupakan bangun yang istimewa, maka segitiga ini mempunyai beberapa hal penting mengenai kongruen. yaitu:

Sisi – Sudut – Sisi
Dua buah segitiga kongruen jika dan hanya jika dua sisi dan sudut apitnya yang berpadanan sama besar.


Sudut – Sisi – Sudut
Dua buah segitiga kongruen jika dan hanya jika satu sisi diketahui dan dua sudut yang ada di sisi tersebut juga sama besar.


Sisi – Sisi – Sisi
Dua buah segitiga dikatakan kongruen jika dan hanya jika ketiga sisinya sama panjang.