Merasionalkan penyebut bentuk akar pangkat dua sudah sering kita jumpai, namun merasionalkan bentuk akar pangkat tiga barangkali jarang kita jumpai, karena tidak semua buku matematika SMA membahas tentang ini.
Pertama yang perlu kita perhatikan definisi dari sekawan. Selama ini di buku-buku dijelaskan bahwa sekawan dari (a - b) adalah (a + b), dan sebaliknya. Definisi ini perlu kita kembangkan sebagai berikut: Dua bentuk akar dikatakan sekawan bila kedua bentuk akar itu dikalikan menjadi bilangan rasional.
Misal:
-
dan
adalah sekawan, karena bila kedua bentuk akar ini dikalikan hasilnya
(Rasional).
dan
adalah sekawan, karena bila kedua bentuk akar ini bila dikalikan hasilnya 2 (ingat rumus (a - b)(a + b)).
dan
adalah sekawan, karena hasil kalinya adalah 3. Gunakan rumus
. Untuk contoh 3 perlu dijelaskan:
= ( )(
)(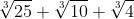 )
)
= ( )(
)(^{2}%20+%20\sqrt[3]{5}\sqrt[3]{2}%20+%20(\sqrt[3]{})^{2}) )
)
= ^{3}%20-%20(\sqrt[3]{2})^{3})
= 5 - 2
= 3
Konsep ini nanti kita gunakan untuk merasionalkan penyebut bentuk akar pangkat tiga
Contoh Soal:
Rasionalkan bentuk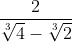 !
!
Penyelesaian:
}{2}=\sqrt[3]{16}+\sqrt[3]{8}+\sqrt[3]{4})