Pertidaksamaan irasional adalah pertidaksamaan yang memuat tanda akar, misal 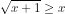 . Menyelesaikan persamaan irasional memerlukan kehati-hatian, bila tidak kita kadang merasa yakin benar, namun ternyata salah. Yang perlu diperhatikan adalah dalam hal memberi batasan (syarat), baik batasan di bawah tanda akar maupun batasan ketika mengkuadratkan kedua ruas.
. Menyelesaikan persamaan irasional memerlukan kehati-hatian, bila tidak kita kadang merasa yakin benar, namun ternyata salah. Yang perlu diperhatikan adalah dalam hal memberi batasan (syarat), baik batasan di bawah tanda akar maupun batasan ketika mengkuadratkan kedua ruas.
Perhatikan contoh-contoh berikut ini!
Perhatikan contoh-contoh berikut ini!
Contoh 1
Carilah semua x yang memenuhi 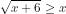
Penyelesaian:
Syarat dibawah tanda akar adalah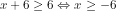
Syarat untuk mengkuadratkan kedua ruas harus postif atau 0 (tidak negatif). Ruas kiri memuat akar berarti nilainya selalu positif atau 0. Ruas kanan harus .
.
Kedua syarat ini kita interseksikan menjadi .
.
Kuadratkan kedua ruas, maka pertidaksamaan menjadi:
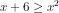
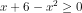
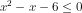
(x-3)\leq%200)
Jadi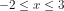
Karena syaratnya maka
maka 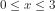 .
.
Sampai di sini belum selesai. Coba perhatikan pertidaksamaan diatas! Ruas kiri yaitu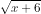 nilainya selau positif, sehingga ruas kanan, yaitu x akan memenuhi pertidaksamaan bila nilainya negatif, sehingga
nilainya selau positif, sehingga ruas kanan, yaitu x akan memenuhi pertidaksamaan bila nilainya negatif, sehingga 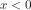 dan
dan 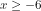 (batasan dibawah tanda akar) juga memenuhi pertidaksamaan.
(batasan dibawah tanda akar) juga memenuhi pertidaksamaan. 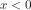 dan
dan 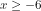 ekuivalen dengan
ekuivalen dengan 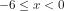
Jadi penyelesaiannya adalah gabungan dari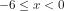 dan
dan 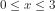 .menjadi
.menjadi 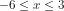
Contoh 2
Tentukan banyak penyelesaian bilangan bulat dari
Penyelesaian:
 ekuivalen dengan
ekuivalen dengan 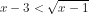
Syarat dibawah tanda akar adalah atau
atau 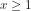
Syarat mengkuadratkan adalah kedua ruas harus positif atau 0. Ruas kanan pasti positif atau nol. Ruas kiri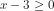 atau
atau  . Kedua syarat ini menjadi
. Kedua syarat ini menjadi  .
.
Kuadratkan kedua ruas menjadi
x2- 6x + 9 < x - 1
x2- 6x + 9 - x + 1 < 0
x2-7x + 10 < 0
(x - 2)(x - 5) < 0
2 < x < 5
Jadi penyelesaiannya adalah 3 dan 4. Batasannya adalah . Jadi sudah sesuai.
. Jadi sudah sesuai.
Sekarang perhatikan pertidaksamaan di atas, yaitu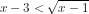 . Pada ruas kanan nilainya selalu positif atau nol, sehingga untuk ruas kiri negatif maka memenuhi pertidaksamaan, Dengan demikian
. Pada ruas kanan nilainya selalu positif atau nol, sehingga untuk ruas kiri negatif maka memenuhi pertidaksamaan, Dengan demikian 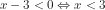 dan
dan 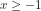 (batasan di bawah tanda akar) juga memenuhi pertidaksamaan.
(batasan di bawah tanda akar) juga memenuhi pertidaksamaan. 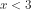 dan
dan 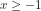 ekuivalen dengan
ekuivalen dengan  . Jadi 1 dan 2 juga merupakan penyelesaian pertidaksamaan. Jadi penyelesaiannya adalah, 1, 2, 3, dan 4. Banyak penyelesaian bilangan bulat sebanyak 4.
. Jadi 1 dan 2 juga merupakan penyelesaian pertidaksamaan. Jadi penyelesaiannya adalah, 1, 2, 3, dan 4. Banyak penyelesaian bilangan bulat sebanyak 4.
Menyelesaikan pertidaksamaan irasional harus memperhatikan batasan (syarat) yang perlu diberikan, yaitu batasan di bawah tanda akar dan batasan ketika mengkuadratkan. Kita sering melupakan mengenai batasan, sehingga penyelesaian suatu pertidaksamaan menjadi salah, walaupun sepertinya langkah-langkah penyelesaian tidak ada yang salah.
Penyelesaian:
Syarat dibawah tanda akar adalah
Syarat untuk mengkuadratkan kedua ruas harus postif atau 0 (tidak negatif). Ruas kiri memuat akar berarti nilainya selalu positif atau 0. Ruas kanan harus
Kedua syarat ini kita interseksikan menjadi
Kuadratkan kedua ruas, maka pertidaksamaan menjadi:
Jadi
Karena syaratnya
Sampai di sini belum selesai. Coba perhatikan pertidaksamaan diatas! Ruas kiri yaitu
Jadi penyelesaiannya adalah gabungan dari
Contoh 2
Tentukan banyak penyelesaian bilangan bulat dari
Penyelesaian:
Syarat dibawah tanda akar adalah
Syarat mengkuadratkan adalah kedua ruas harus positif atau 0. Ruas kanan pasti positif atau nol. Ruas kiri
Kuadratkan kedua ruas menjadi
x2- 6x + 9 < x - 1
x2- 6x + 9 - x + 1 < 0
x2-7x + 10 < 0
(x - 2)(x - 5) < 0
2 < x < 5
Jadi penyelesaiannya adalah 3 dan 4. Batasannya adalah
Sekarang perhatikan pertidaksamaan di atas, yaitu
Menyelesaikan pertidaksamaan irasional harus memperhatikan batasan (syarat) yang perlu diberikan, yaitu batasan di bawah tanda akar dan batasan ketika mengkuadratkan. Kita sering melupakan mengenai batasan, sehingga penyelesaian suatu pertidaksamaan menjadi salah, walaupun sepertinya langkah-langkah penyelesaian tidak ada yang salah.
